Monotonic Constraints
It is often the case in a modeling problem or project that the functional form of an acceptable model is constrained in some way. This may happen due to business considerations, or because of the type of scientific question being investigated. In some cases, where there is a very strong prior belief that the true relationship has some quality, constraints can be used to improve the predictive performance of the model.
A common type of constraint in this situation is that certain features bear a monotonic relationship to the predicted response:
whenever \(x \leq x'\) is an increasing constraint; or
whenever \(x \leq x'\) is a decreasing constraint.
XGBoost has the ability to enforce monotonicity constraints on any features used in a boosted model.
A Simple Example
To illustrate, let’s create some simulated data with two features and a response according to the following scheme
The response generally increases with respect to the \(x_1\) feature, but a sinusoidal variation has been superimposed, resulting in the true effect being non-monotonic. For the \(x_2\) feature the variation is decreasing with a sinusoidal variation.
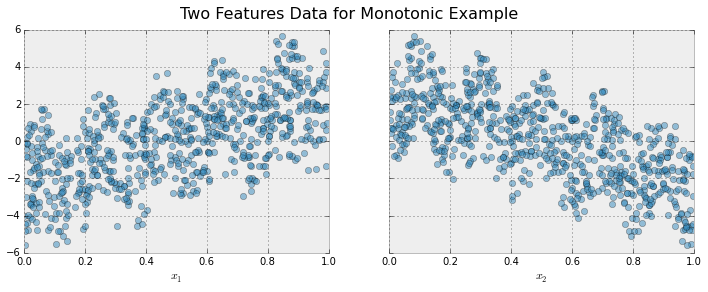
Let’s fit a boosted tree model to this data without imposing any monotonic constraints:
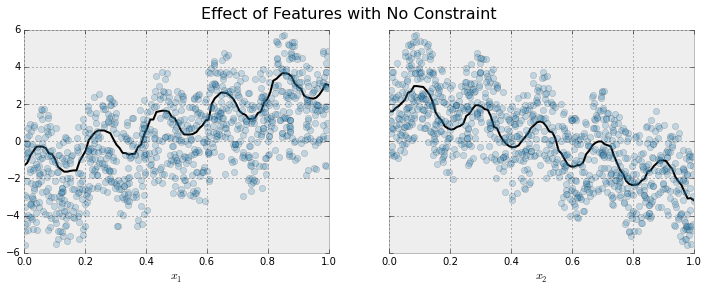
The black curve shows the trend inferred from the model for each feature. To make these plots the distinguished feature \(x_i\) is fed to the model over a one-dimensional grid of values, while all the other features (in this case only one other feature) are set to their average values. We see that the model does a good job of capturing the general trend with the oscillatory wave superimposed.
Here is the same model, but fit with monotonicity constraints:
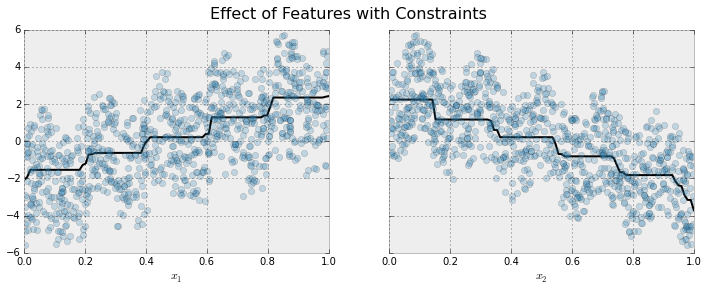
We see the effect of the constraint. For each variable the general direction of the trend is still evident, but the oscillatory behaviour no longer remains as it would violate our imposed constraints.
Enforcing Monotonic Constraints in XGBoost
It is very simple to enforce monotonicity constraints in XGBoost. Here we will give an example using Python, but the same general idea generalizes to other platforms.
Suppose the following code fits your model without monotonicity constraints
model_no_constraints = xgb.train(params, dtrain,
num_boost_round = 1000, evals = evallist,
early_stopping_rounds = 10)
Then fitting with monotonicity constraints only requires adding a single parameter
params_constrained = params.copy()
params_constrained['monotone_constraints'] = (1,-1)
model_with_constraints = xgb.train(params_constrained, dtrain,
num_boost_round = 1000, evals = evallist,
early_stopping_rounds = 10)
In this example the training data X has two columns, and by using the parameter values (1,-1) we are telling XGBoost to impose an increasing constraint on the first predictor and a decreasing constraint on the second.
Some other examples:
(1,0): An increasing constraint on the first predictor and no constraint on the second.(0,-1): No constraint on the first predictor and a decreasing constraint on the second.
Note
Note for the ‘hist’ tree construction algorithm. If tree_method is set to
either hist or approx, enabling monotonic constraints may produce unnecessarily
shallow trees. This is because the hist method reduces the number of candidate
splits to be considered at each split. Monotonic constraints may wipe out all available
split candidates, in which case no split is made. To reduce the effect, you may want to
increase the max_bin parameter to consider more split candidates.
Using feature names
XGBoost’s Python package supports using feature names instead of feature index for
specifying the constraints. Given a data frame with columns ["f0", "f1", "f2"], the
monotonic constraint can be specified as {"f0": 1, "f2": -1}, and "f1" will
default to 0 (no constraint).